Revisiting the BART Algorithm
Stephen Brennan • 11 December 2016Over the summer I wrote about my hackathon project, an app that virtually swaps BART tickets in order to reduce fares. This was a purely academic exercise, to apply some concepts I had learned from my “Advanced Algorithms” course to a problem in the real world. I described how you could model this problem as an (integer) linear program, and I guessed that the problem is, in fact, totally unimodular. However I offered no proof of this, and due to hackathon time constraints I was forced to use a slow, somewhat half-baked greedy algorithm to solve the problem.
With this article I want to rectify some of those problems. In particular, I’ll describe what went wrong in my initial linear programming formulation and how I have fixed it. Then, I’ll describe the similarities between this problem and the minimum cost network flow problem. Finally, I’ll give actual argument that the constraint matrix of this problem is totally unimodular, so we can feel better about using a linear programming solver.
Problem Definition
The Cliff’s Notes version of my last article is as follows. At any given time, a lot of people are traveling between stations on the BART train system. Normally, each person buys a ticket for the starting and ending stations of their own trip. However, if we look at the system as a whole, there’s usually a better (i.e. cheaper) way to buy tickets so that each station has the same number of travelers entering and exiting that station. In magical theory world, everyone could be assigned a ticket on entry and then a separate ticket on exit. In the real world, this would result in lots of people swapping tickets on platforms, or else some sort of electronic Clipper Card spoofing that’s not currently practical.
The linear programming formulation is simple. If 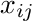 represents the
number of tickets purchased from station
represents the
number of tickets purchased from station 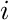 to
to 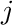 , and
, and 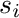 represents
the number of travelers departing from station
represents
the number of travelers departing from station 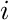 , and
, and 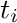 represents the
number of travelers arriving at station
represents the
number of travelers arriving at station 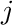 , then we have two sets of
constraints:
, then we have two sets of
constraints:
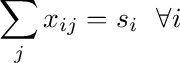
This represents the constraint that the tickets starting at 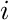 need to add up
to the number of travelers departing from
need to add up
to the number of travelers departing from 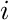 .
.
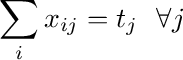
This represents the constraint that the tickets destined for 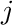 need to add
up to the number of travelers arriving at
need to add
up to the number of travelers arriving at 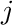 . You can combine these
constraints into the matrix form
. You can combine these
constraints into the matrix form 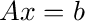 quite easily. We can define
quite easily. We can define 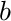 as
simply a vector containing all
as
simply a vector containing all 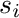 followed by all
followed by all 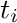 . The vector
. The vector 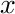 will contain the variables
will contain the variables 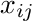 in row-major order. The matrix
in row-major order. The matrix 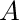 is
best visualized by the following table, for a simple 3-station example.
is
best visualized by the following table, for a simple 3-station example.
| 11 | 12 | 13 | 21 | 22 | 23 | 31 | 32 | 33 | |
|---|---|---|---|---|---|---|---|---|---|
| Starts at 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Starts at 2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Starts at 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| Ends at 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| Ends at 2 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| Ends at 3 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
The other constraints are that the 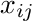 need to be positive integers. That
“integer” part makes this an integer linear program, which is much harder to
solve than a normal one, unless you happen to have a totally unimodular problem.
We’ll get to that in a moment.
need to be positive integers. That
“integer” part makes this an integer linear program, which is much harder to
solve than a normal one, unless you happen to have a totally unimodular problem.
We’ll get to that in a moment.
Failure To Solve
In my previous article, after describing this formulation, I talked about how the SciPy linear programming solver wasn’t solving this linear program properly. This being a hackathon, I banged my head against the keyboard a few times in frustration, blamed anything that wasn’t me, and went full Rambo, implementing my own algorithm. This algorithm actually worked, but it was horrendously slow.
More importantly, I never really stopped to examine the flaw in my logic. An industry-grade implementation of a classic algorithm for solving a well-known class of optimization problems was just wrong on my input?
Nope. I did something wrong.
You see, most approaches to solving a linear program expect that your constraints are linearly independent. That is, you can’t write one constraint by summing and/or subtracting other constraints. My implementation included all 45 BART stations regardless of whether there were any travelers using those stations. With all of those extra constraints, if I entered some small test case, the solver would fail miserably because of linearly dependent constraints. Admittedly, some better error messages would have been nice, but ultimately this was my fault.
Recently I’ve improved my old SciPy based solver. Now it only includes in the linear program those stations which have travelers departing or arriving. So far I haven’t encountered any problems with this corrected implementation. It produces the same results as my previous implementation, and it runs an order of magnitude quicker (a minute or less versus around 40 minutes). This updated implementation can be found at the GitHub repository.
Is This Just Minimum Cost Flow?
One person left a comment on my previous article saying that this problem can be modeled as minimum cost flow. This is true, and since I also studied minimum cost flow in my advanced algorithms class, I thought it would be fun to demonstrate that, at least intuitively, in this article.
First, the definition of minimum cost flow. The basic idea is that you have a directed graph which has a “source” and a “sink” node. The goal of this problem is to send a certain amount of flow along the directed edges from the source to the sink. However, each edge has a cost per unit of flow associated with it, as well as a capacity (i.e. maximum amount of flow) and even potentially a minimum required amount of flow. So the goal of the whole problem is to send the flow so that you minimize your cost while satisfying the capacity and lower bound constraints.
There are a lot of similarities between these two problems right off the bat. We have a directed, fully connected graph, and we’re trying to send a flow (of travelers) through this graph. Each pair of nodes (stations) has an associated cost. There’s no theoretical upper bound to the number of people traveling between two stations—although practically you can only fit so many people on a train. However, the one glaring difference is that we have many “sources” and “sinks.”
We could easily take this BART problem and turn it into a Minimum Cost Flow problem by adding two new nodes: a source and sink. All travelers entering BART would start from the source node, and all travelers leaving BART would exit through the sink node. There would be a zero-cost edge connecting the source to each station, and it would have a lower bound equal to the number of travelers entering that station. Similarly, there would be a zero-cost edge from each station to the sink node, with a lower bound equal to the number of travelers leaving that station.
So in a nutshell, yes, this problem does reduce to minimum cost flow. But, it requires a bit of a transformation to get there.
Total Unimodularity
As I described in my original article, when you know that the constraint matrix of a linear program is totally unimodular, you know that you can relax the integer constraint on the problem, since the optimal solution is guaranteed to be integer anyway.
All minimum cost flow linear programs are totally unimodular. Our problem can be
transformed into a minimum cost flow problem. However, the linear program we
made up and the linear program we would get from the minimum cost flow version
of the problem are not the same (there are at least 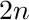 more variables in the
minimum cost flow version: one for each arc between the source/sink and the
stations). So even though we know that our linear program should have a
totally unimodular constraint matrix, we don’t have a solid argument relying
solely on the constraint matrix.
more variables in the
minimum cost flow version: one for each arc between the source/sink and the
stations). So even though we know that our linear program should have a
totally unimodular constraint matrix, we don’t have a solid argument relying
solely on the constraint matrix.
Thankfully, it’s not too hard. Quoting the Wikipedia1 article on Unimodularity:
Let
be a
by
matrix whose rows can be partitioned into two disjoint sets
and
. Then, the following four conditions together are sufficient for
to be totally unimodular:
Every column of
contains at most two non-zero entries.
Every entry in
is 0, +1, or -1.
If two non-zero entries in a column of
have the same sign, then the row of one is in
, and the other is in
.
If two non-zero entries in a column of
have opposite signs, then the rows of both are in
, or both in
.
Our constraint matrix satisfies this exactly! Let’s take this step by step.
- Every column of
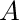 does contain at most two non-zero entries, because each
column appears in exactly two constraints: one for the starting station and
one for the ending station.
does contain at most two non-zero entries, because each
column appears in exactly two constraints: one for the starting station and
one for the ending station. - Every entry of
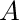 is either 0 or 1.
is either 0 or 1. - If we let
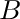 be the set of rows corresponding to the source constraints,
and
be the set of rows corresponding to the source constraints,
and  be the set of rows corresponding to the destination constraints,
then each pair of constraints will be assigned properly.
be the set of rows corresponding to the destination constraints,
then each pair of constraints will be assigned properly. - There are no opposite sign entries!
Now we can have that warm, fuzzy feeling inside telling us that we have math on our side.
Lessons Learned
I think there are a few things I’ve learned from this. Hackathons can be neat, but they’ve always bothered me because of how they encourage exactly the sort of thinking I fell victim to. With such a short time constraint between me and demo time, I had to ditch the more theoretically sound approach to my problem in favor of an ad-hoc algorithm I knew I could get to work in time. What’s worse, I placed the blame on the SciPy solver rather than myself, since I hadn’t figured out what I did wrong. I think everyone, starting with me, can do with a more critical eye to their own code, and I think the hackathon mindset frequently stands in the way of that.
That being said, I don’t want to hate on hackathons too much. They are a fun way to blow off some steam and get a chance to try that wild and crazy idea you had.
Footnotes
-
For those who would complain about Wikipedia as a source: I followed the reference for this particular proof, all the way to a book which I could find no version of online (even through my university’s online resources). I tracked it down in the stacks of the library and found the exact theorem and proof! It’s pretty satisfying. You can read it too: Kuhn, H.W.; Tucker, A.W., Linear Inequalities and Related Systems, Annals of Mathematics Studies, 38, Princeton (NJ): Princeton University Press, pp. 252-253. ↩

Stephen Brennan's Blog is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License